Considere duas estrelas de um sistema binário em que cada qual descreve um órbita circular em torno do centro de massa comum. Sobre tal sistema são feitas as seguintes afirmações:
I. O período de revolução é o mesmo para as duas estrelas.
II. Esse período é função apenas da constante gravitacional, da massa total do sistema e da distância entre ambas as estrelas.
III. Sendo R1 e R2 os vetores posição que unem o centro e massa dos sistema aos respectivos centros de massa das estrelas, tanto R1 como R2 varrem áreas de mesma magnitude num mesmo intervalo de tempo.
Assinale a alternativa correta.
A) Apenas a afirmação I é verdadeira.
B) Apenas a afirmação II é verdadeira.
C) Apenas a afirmação III é verdadeira.
D) Apenas as afirmações I e II são verdadeiras.
E) Apenas as afirmações I e III são verdadeiras.
-------------------------------------------------------------------------------------------------- RESPOSTA: D
Resposta Comentada:
I. (VERDADEIRA)
Análise qualitativa: se um sistema é composto apenas por duas massas e elas descrevem órbitas circulares em torno de um centro de massa comum, elas devem ter o mesmo período orbital.
Análise quantitativa:
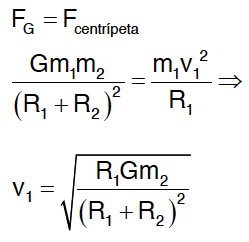
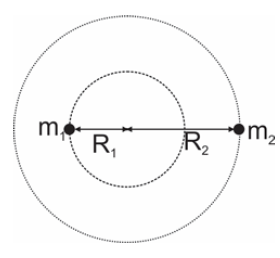
O período do movimento é dado por:
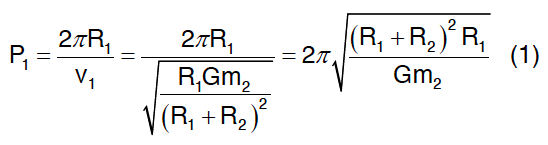
Analogamente:
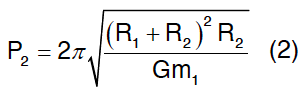
Dado que o centro das órbitas é também o centro de massa do sistema:
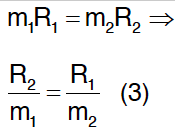
Das equações (3), (2) e (1), concluímos que P1 = P2.
II. (VERDADEIRA)
Da equação (3)

Substituindo (4) em (1):

III. (FALSA)
A velocidade areolar é dada por:
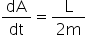 , em que L é a quantidade de movimento angular.
, em que L é a quantidade de movimento angular.
Assim, 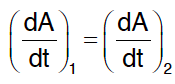 apenas se R1 = R2.
apenas se R1 = R2.
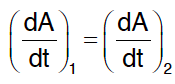 apenas se R1 = R2.
apenas se R1 = R2.

Nenhum comentário:
Postar um comentário