(IME 2017) - QUESTÃO

O sistema de inequações abaixo admite k soluções inteiras. Pode-se afirmar que:

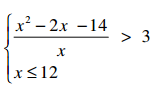
a) 0 ≤ k < 2 

b) 2 ≤ k < 4 

c) 4 ≤ k < 6 

d) 6 ≤ k < 8

e) k ≥ 8

-------------------------------------------------------------------------------------------------- RESPOSTA: D
Resposta Comentada:

A primeira inequação é equivalente 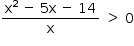a 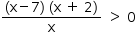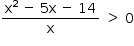, ou seja, .

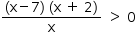Analisando os possíveis intervalos, temos:

  

Logo, – 2 < x < 0 ou x > 7.

Juntando com x  ≤ 12, segue que o conjunto solução é 

As soluções inteiras são – 1, 8, 9, 10, 11, 12 e, portanto, k = 6.