Sejam Z1 e Z2 números complexos tais que Z2 é imaginário puro e |Z1 − Z2|=| Z2| . Para quaisquer valores de Z1 e Z2 que atendam a essas condições tem-se que:
a) Im(Z2) > 0
b) Im(Z2) ≤ 0
c) Z1| ≤ 2 | Z2|
d) Re(Z1) ≥ 0
e) Re(Z1) ≤ Im(Z2)
Resposta Comentada:
Como 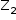 é imaginário puro, ele está localizado no eixo imaginário do plano de Argand-Gauss.
é imaginário puro, ele está localizado no eixo imaginário do plano de Argand-Gauss.
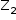 é imaginário puro, ele está localizado no eixo imaginário do plano de Argand-Gauss.
é imaginário puro, ele está localizado no eixo imaginário do plano de Argand-Gauss.
Como 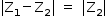 ,
, 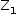 está localizado em uma circunferência de raio
está localizado em uma circunferência de raio 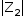 centrada em
centrada em 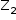 , que tangencia o eixo real na origem.
, que tangencia o eixo real na origem.
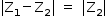 ,
, 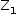 está localizado em uma circunferência de raio
está localizado em uma circunferência de raio 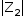 centrada em
centrada em 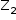 , que tangencia o eixo real na origem.
, que tangencia o eixo real na origem.
Como 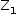 e
e 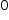 estão na circunferência, a distância entre eles é menor ou igual ao diâmetro e então:
estão na circunferência, a distância entre eles é menor ou igual ao diâmetro e então:
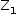 e
e 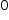 estão na circunferência, a distância entre eles é menor ou igual ao diâmetro e então:
estão na circunferência, a distância entre eles é menor ou igual ao diâmetro e então: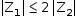 .
.

Nenhum comentário:
Postar um comentário