(IME 2017) - QUESTÃO

Seja

 

com a ∈ ℜ . Sabe-se que det(A² − 2A + ℓ) = 16. A soma dos valores de a que satisfazem essa condição é:

Obs: det(X) denota o determinante da matriz X

a) 0

b) 1

c) 2

d) 3

e) 4

-------------------------------------------------------------------------------------------------- RESPOSTA: D
Resposta Comentada:

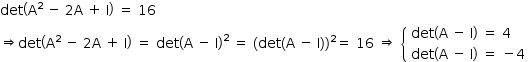
• Calculando det(A – I)

• 1° caso: det(A – I) = 4 ⇒ 8a – 12 = 4 ⇒ 8a = 16 ⇒ a1 = 2
• 2º caso: det(A – I) = –4 ⇒ 8a – 12 = –4 ⇒ 8a = 8 ⇒ a2 = 1

Soma = a1 + a2 = 1 + 2 = 3