(IME 2017) - QUESTÃO

O polinômio P(x) = x³ − bx² + 80x − c possui três raízes inteiras positivas distintas. Sabe-se que duas das raízes do polinômio são divisoras de 80 e que o produto dos divisores positivos de c menores do que c é c². Qual é o valor de b?

a) 11 

b) 13 

c) 17 

d) 23 

e) 29

-------------------------------------------------------------------------------------------------- RESPOSTA: E
Resposta Comentada:

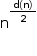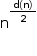O produto dos divisores positivos de n é , onde d(n) é o número de divisores positivos de n.

Pelo enunciado, o produto de todos os divisores positivos é c2 · c = c3. Logo, d(c) = 6, e então c é da forma p5ou p2q, onde p e q são primos distintos.

Sendo r1, r2, r3 as raízes do polinômio, temos r1 r2 r3 = c.

Caso 1: c = p5

Poderíamos ter p = 2 ou p = 5, mas nenhum desses valores satisfaz a equação.

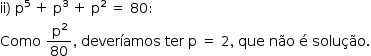
Caso 2: c = p2q

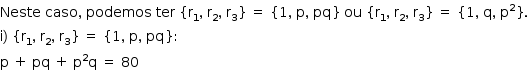
Podemos ter p = 2 ou p = 5. Se p = 5, teríamos 30q = 75, o que é absurdo. Se p = 2, teríamos 6 q = 78 ⇔ q = 13.

Logo, as raízes são 1, 2 e 26, o que nos dá b = 29.

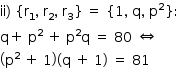
Se p = 2, teríamos 5(q + 1) = 81, o que é absurdo.

Se p ≠ 2, p é ímpar, e então (p2 + 1) (q + 1) é par, o que é absurdo.

Logo, a única possibilidade é, de fato, {r1, r2, r3} = {1, 2, 26}.