(IME 2017) - QUESTÃO

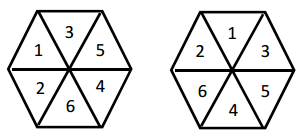
Um hexágono é dividido em 6 triângulos equiláteros. De quantas formas podemos colocar os números de 1 a 6 em cada triângulo, sem repetição, de maneira que a soma dos números em três triângulos adjacentes seja sempre múltiplo de 3? Soluções obtidas por rotação ou reflexão são diferentes, portanto as figuras abaixo mostram duas soluções distintas.

a) 12 

b) 24 

c) 36 

d) 48 

e) 96


-------------------------------------------------------------------------------------------------- RESPOSTA: D
Resposta Comentada:

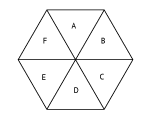
Temos A + B + C ≡ 0 (mód 3) e B + C + D ≡ 0 (mód 3), o que nos dá A ≡ D (mód 3).

Analogamente, B ≡ E (mód 3) e C ≡ F (mód 3).

Como de 1 até 6 temos 2 números em cada classe de congruência módulo 3, segue que A e D estão na mesma classe, bem como B e E e C e F.

Reciprocamente, se essas condições são satisfeitas, a soma de cada três consecutivos é múltipla de 3.

Temos 3! maneiras de permutar as classes e 2! maneiras de permutar dentro de cada classe.

Logo, o número de maneiras é 3! · (2!)3 = 48.